

This formula can be used when you know and want to determine the sample size necessary to establish, with a confidence of, the mean value to within. Rearranging this formula, we can solve for the sample size necessary to produce results accurate to a specified confidence and margin of error. Is known as the critical value, the positive value that is at the vertical boundary for the area of in the right tail of the standard normal distribution. Handpicked Content: Eliminating the Fear About Using Confidence Intervals
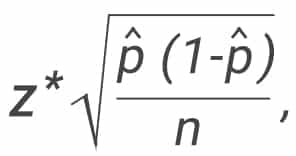
The margin of error is the maximum difference between the observed sample mean and the true value of the population mean : This difference between the sample and population means can be thought of as an error. When sample data is collected and the sample mean is calculated, that sample mean is typically different from the population mean. In many cases, we can easily determine the minimum sample size needed to estimate a process parameter, such as the population mean.

If data is not readily available for the process, how many members of the population should be selected to ensure that the population is properly represented? If data has been collected, how do you determine if you have enough data?ĭetermining sample size is a very important issue because samples that are too large may waste time, resources and money, while samples that are too small may lead to inaccurate results. This allows you to quantify the process improvement (e.g., defect reduction or productivity increase) and translate the effects into an estimated financial result – something business leaders can understand and appreciate. In order to prove that a process has been improved, you must measure the process capability before and after improvements are implemented.


 0 kommentar(er)
0 kommentar(er)
